Квантна декохеренција

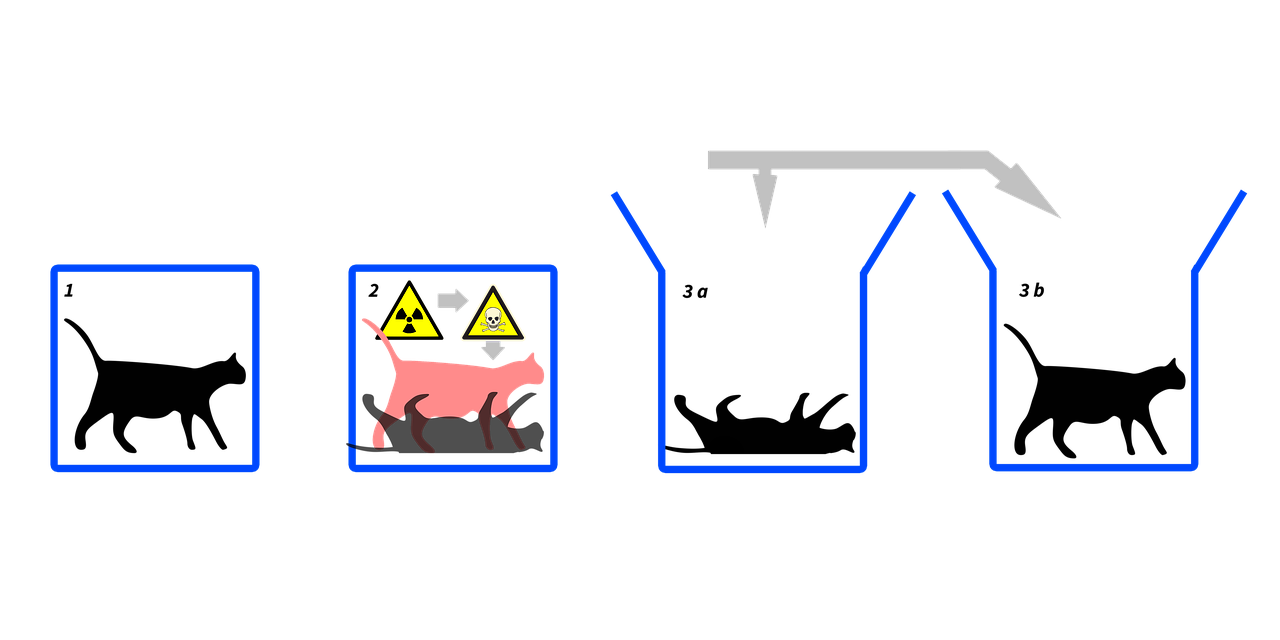
Реални физички системи интерагују са другим физичким системима који се збирно могу назвати окружењем. Интеракција једног квантног бита (кубита) са својим окружењем може довести до промене стања кубита: \[|\psi\rangle=c_0|0\rangle+c_1|1\rangle\rightarrow |0\rangle\tag{1}\] као и до промене \[|\psi\rangle=c_0|0\rangle+c_1|1\rangle\rightarrow |1\rangle.\tag{2}\] До које од ових двеју промена, (1), или (2), ће доћи се не може унапред рећи. Сваки појединачни кубит доживљава, или промену (1), или промену (2). Зато се на скупу кубитова, свих у истом почетном стању \(|\psi\rangle\), може говорити само помоћу вероватноће промене стања. Вероватноћа промене стања датa изразом (1) износи \(|c_0 |^2\), а промене стања дата изразом (2) износи \(|c_1 |^2=1-|c_0 |^2\).

Исто важи и за пар кубита у почетном сплетеном стању: интеракција било којег од кубита са окружењем може довести (баш као у поступку мерења ), за сваки појединачни кубит, \[|\Psi\rangle=\frac{1}{\sqrt{2}}(|0\rangle|1\rangle-|1\rangle|0\rangle)\rightarrow|0\rangle|1\rangle\tag{3}\] или до промене \[|\Psi\rangle=\frac{1}{\sqrt{2}}(|0\rangle|1\rangle-|1\rangle|0\rangle)\rightarrow|1\rangle|0\rangle\tag{4}\] и то свака од ових промена стања са вероватноћом једнаком \(\frac{1}{2}=(\pm\frac{1}{\sqrt{2}})^2\).

Историјски, у теорији и тумачењу (интерпретацији) процеса квантног мерења, промене стања (1)-(4) су познате као „редукција стања“ (state reduction), или „колапс стања“ (state collapse). А те промене су фасцинантне, нпр. изрази (1) и (2):

Сваки појединачни кубит губи почетну кохеренцију – то јест, суперпозицију стања – и на крају се нађе у само једном од почетно суперпонираних стања.

Ово губљење квантне кохеренције (суперпозиције стања) се данас назива процесом (ефектом) квантне декохеренције.

Гледајући, на пример, десну страну у изразима (3) и (4), препознајемо неке чланове из Схеме 2 у оквиру упознавања са квантном сплетеношћу. За сва стања представљена у Схеми 2 већ смо рекли да су у потпуности аналогна класичним записима датим Схемом 1 у истој презентацији. Дакле, стања \(|0\rangle|1\rangle\) и \(|1\rangle|0\rangle\) из израза (3) и (4) можемо препознати као класично-слична („ базис израчунавања“), то јест, ту нема пуне квантности исказане квантно сплетеним стањем \(|\Psi\rangle\) које носи квантну кохеренцију.

Сво информатичко баратање стањима која су из „базиса израчунавања“, делимично датом на десној страни израза (3)-(4), не носи квантни ресурс и у том смислу је класично (прецизније: слично класичном). Зато се и не очекује да баратање кубитовима у стањима из базиса израчунавања донесе неку предност квантног у односу на класично процесирање информација, или рачунање.

Квантни рачунари изложени квантној декохеренцији постају (у реченом смислу) класични.