Квантне технологије
Квантна физика и квантне технологије
придружите се
Квантна нелокалност
Квантна физика
Размотримо пар кубита (квантних битова). Одаберимо „базис израчунавања“ (рецимо вртње око \(x\) осе – у једном смеру је \(0\), у супротном \(1\)), \(|0\rangle\) и \(|1\rangle\). Тада (и независно од тога да ли има корелација између кубита) важи рецептура, на пример: „први кубит се налази у стању \(|0\rangle\) , а други кубит се налази у стању \(|1\rangle\)"\(\leftrightarrow |0\rangle|1\rangle\). Међутим, општије, сплетено стање пара кубита, неко \(|\Psi\rangle\), може да гласи: \[\frac{1}{\sqrt{2}}(|+\rangle|-\rangle-|-\rangle|+\rangle)=|\Psi\rangle=\frac{1}{\sqrt{2}}(|0\rangle|1\rangle-|1\rangle|0\rangle)\tag{1}\] где стања на левој страни израза (1) одговарају вртњама око неке друге осе која није \(x\) оса.
Поређење леве и десне стране израза (1) сугерише да горе дата рецептура не може бити примењена на стање (1). Са десне стране се налазе стања која одговарају вртњи око \(x\) осе, док се на левој страни истог израза (1) налазе вртње око неке друге осе – класично забрањено. И заиста, може се строго показати да кубити, појединачно, немају одређена своја квантна стања. Тако је први аспект квантне нелокалности, историјски познат као
(Квантна несепарабилност) Квантни подсистеми немају своја квантна стања ако се целина од којих се састоји налази у квантно сплетеном стању (које је једнозначно познато).
Други аспект квантне нелокалности се тиче ентропије (која овде неће бити уведена) и која има необичну особину
(Квантни холизам) Ентропија целине у стању (1) једнака је нули, док непознавање стања подсистема (сходно квантној несепарабилности) води ненултој ентропији за оба подсистема. Дакле, о целини се зна највише што се може (стање је једнозначно познато те је ентропија једнака \(0\)), док постоји мањак (класичне) информације о стањима подсистема (ентропија већа од \(0\) за оба подсистема, тј., оба кубита!).
Трећи аспект се тиче поступка мерења и тренутне промене стања подсистема на којем се мерење не обавља.
Да бисмо то увидели, ево рецептуре која се у квантној механици успоставља за једну врсту квантних мерења.
Ако је целина у стању (1), добијање резултата који одговара мерењу на првом кубиту исказаном стањем, на пример, \(|-\rangle\), води промени стања целине
\[|\Psi\rangle\rightarrow|-\rangle|+\rangle\tag{2}\]
Тиме је: (А) На почетку мерења стање целине било \(|\Psi\rangle\), а стања подсистема нису била дефинисана, док (Б) После мерења, УСЛЕД мерења, је истовремено (тренутно)
успостављено* коначно стање целине (израз (2)), али и коначно стање првог кубита (стање \(|-\rangle\)), као и коначно стање \(|+\rangle\) другог кубита (на којем се мерење не обавља).
С обзиром да растојање између два кубита може бити произвољно велико, овај аспект квантне нелокалности се често назива
(Дистантне корелације) У квантном мерењу коначна стања свих квантних подсистема се истовремено (тренутно) успостављају.
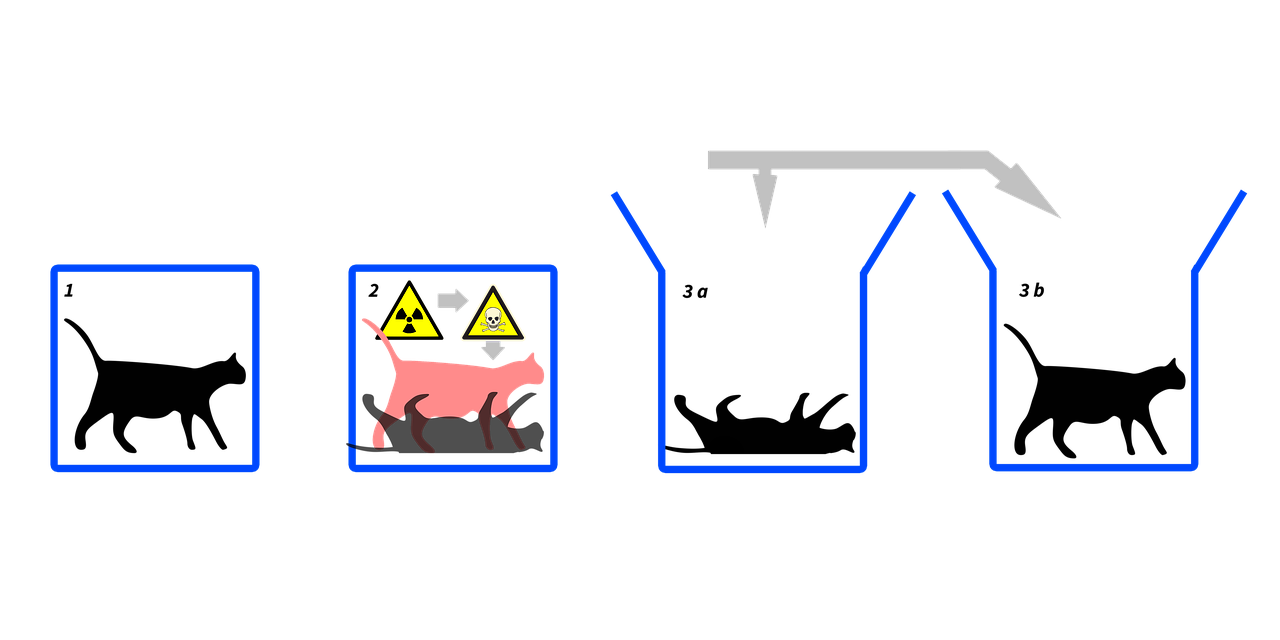
Од суштинског је значаја схватити: „дистантне корелације“ се тичу и класичних система (и класичних мерења), видети, на пример, Схему 1. Поента овде наведених,
квантних, дистантних корелација као аспекта квантне нелокалности лежи у корелацијама које се тичу нових (класично могуће и забрањених!) стања на левој страни израза (1).
Сви наведени аспекти квантне нелокалности се тичу квантно сплетених стања. Један квантитативни критеријум квантне нелокалности представља нарушење Белове неједнакости.
*Од суштинског је значаја уочити: квантно мерење успоставља стања (и целине, и сваког кубита појединачно, израз (2)). Али у класичном случају, Схема 1, нема никаквог успостављања стања као последица мерења – стање је реално присутно и ничиме није условљено. То јест, класично мерење га не мења, већ само препознаје (обезбеђује информацију) о којем стању је реч.